风电场风机尾流及其迭加模型的研究(2)

    本文针对风电场风机尾流计算与尾流迭加问题，从现有一维线性模型所存在的缺陷入手，建立更完整、合理的一维非线性扩张尾流模型；针对风机尾流迭加的不同情况，建立完整的风机尾流迭加模型；结合相关的工程算例，通过与三维数值模拟计算结果的对比分析，验证了所建立的风机尾流模型及其迭加模型的合理性和适用性。
1 模型推导
1.1 非线性尾流模型
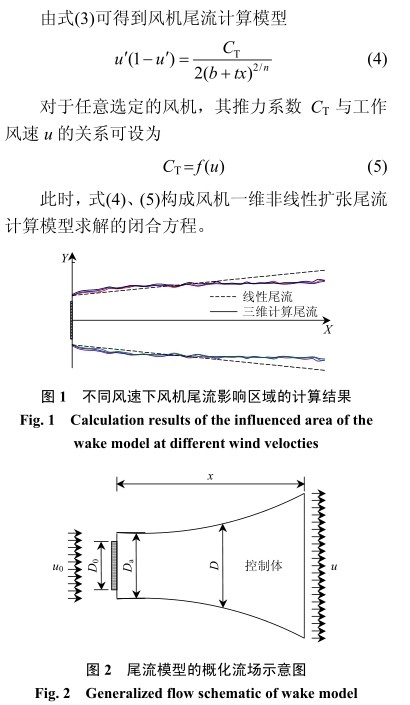
    利用三维计算流体动力学(computational fluiddynamics，CFD)对风电场风机尾流进行模拟分析，结果表明(如图 1 所示)：风机尾流影响直径的变化趋势并非线性，而是趋向于多次抛物线型。采用一维线性尾流模型模拟风机尾流可能存在较大的偏差，其影响主要有：
1）尾流影响直径假设不合理造成风速计算不准确，导致优化的位置达不到最优预期，且随着距离的增大，计算偏差较大；
2）在判断下游风机是否处在上游风机的尾流影响区域内时，由于尾流区域的假设不合理，判断结果将出现偏差。因此，非线性尾流研究主要建立在关注风轮的湍流影响的基础上，克服原有线性尾流模型的弊端， 采用简化风机尾流非线性扩张模型(即尾流影响边界随距离非线性增大)，其简化模型如图 2 所示，该模型风机尾流呈非线性变化趋势。现采用控制体积法对风机流场进行分析，并设：u 0 、u 分别为风机前、风机后距离风机 x 处的风速；D 0 为风轮直径；D a 、D 分别为风机后、距离风机 x 处的尾流直径。根据欧拉输运公式以及动能定理可得

1.2 尾流迭加模型
在一维尾流计算模型 [13-15] 中，目前常用的风机尾流迭加模型有 2 种，均为简化计算模型。一种是采用最大尾流衰减确定受影响风机处的尾流风速，另一种采用动能衰减原理确定受影响风机处的尾流风速。 对于风机尾流的迭加， 应分为 2 种情况 ( 如图 3 所示 ) ：情况 1 ，尾流迭加计算处风机的上游风机处于其他风机的尾流影响范围之内；情况 2 ，尾流迭加计算处风机的上游风机不处于其他风机的尾流影响范围之内。
1 ）针对情况 1 的风机尾流迭加模型的推导。
该情况中，第 n 台风机的尾流风速主要受上游第 n − 1 台风机的影响，上游的 n − 2 台风机只是影响该风机尾流边界的尾流恢复速度，对其尾流风速的影响是间接的。
设风电场 n 台风机沿轴线方向排列，风机工作风速分别记为 u 1 , u 2 ,  , u n ，如图 2(a) 所示。取 1 号风机和 2 号风机部分作为控制体，根据欧拉输运方程可得
T 1  = ρ u 2 (u 1  − u 2 )A 12  = ρ u 12 (u 1  − u 12 )A 12 (6)
式中： u 12 为上游风机 1 在风机 2 处的尾流风速；
A 12 为上游风机 1 在风机 2 处的尾流影响面。

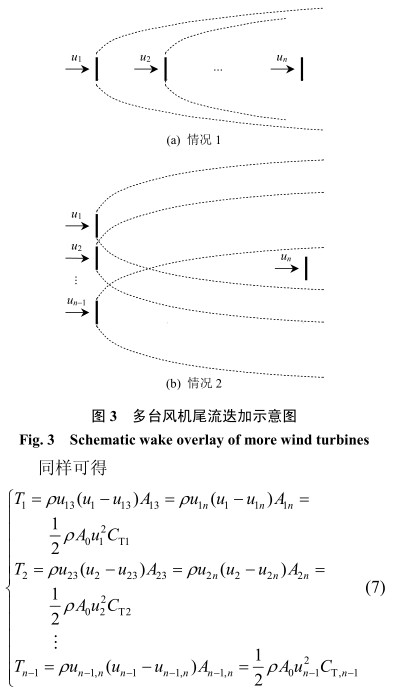
第 n 台风机受上游 n − 1 台风机的尾流影响， 存在 n − 1 个尾流迭加区域。 事实上， 采用一维尾流模型进行尾流的迭加计算时，任意风机处不可能具有一个以上的尾流风速和尾流直径。因此，图 3(a) 所示的尾流影响区域是不可能存在的，风机尾流影响区域的示意图如图 4 所示。
考虑 1 号风机和 n 号风机间的控制体，可得
T 1  + T 2  + ⋅⋅⋅ + T n  = ρ u n ( u n  − u 1 ) A n (8)
联立式 (7) 、 (8) ：

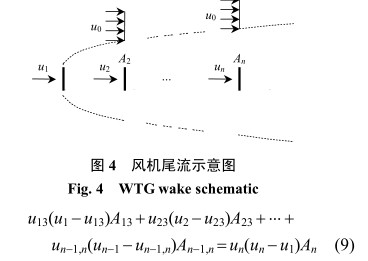
由式 (9) 即可求出第 n 台风机处的尾流风速 u n 。